python二维列表,python静夜思古诗代码

在Python中，二维列表一般指的是列表的列表，即一个列表中包含了多个列表。每个内部列表能够看作是一个一维列表，而外部列表将这些一维列表安排在一起，形成了一个二维结构。这种结构能够用来表明表格数据、矩阵等。

下面是一些关于二维列表的根本操作和示例：

1. 创立二维列表： 能够直接运用嵌套的列表来创立二维列表。 运用列表推导式来创立具有特定形式的二维列表。

2. 拜访二维列表中的元素： 运用两个索引来拜访二维列表中的元素，榜首个索引表明行，第二个索引表明列。

3. 遍历二维列表： 能够运用嵌套循环来遍历二维列表中的每个元素。

4. 修正二维列表中的元素： 直接运用两个索引来修正二维列表中的元素。

5. 扩展或减缩二维列表： 能够经过增加或删去内部列表来扩展或减缩二维列表。

下面是一些示例代码，展现了怎么创立、拜访、遍历和修正二维列表：

```python 创立二维列表matrix = , , qwe2

拜访二维列表中的元素element = matrix 拜访第二行第三列的元素

遍历二维列表for row in matrix: for element in row: print print 换行

修正二维列表中的元素matrix = 10 将榜首行榜首列的元素修正为10

扩展二维列表matrix.appendqwe2 增加一个新行matrix.append 在榜首行结尾增加一个新列```

这些示例展现了二维列表的根本操作，能够依据具体需求进行扩展和修正。

Python二维列表详解

在Python编程中，二维列表是一种十分有用的数据结构，它答应咱们存储和操作具有多行多列的数据。本文将具体介绍Python二维列表的概念、创立办法、操作技巧以及在实践运用中的运用场景。

一、二维列表的概念

什么是二维列表？

二维列表，望文生义，是由多个一维列表组成的列表。每个一维列表能够看作是二维列表的一行，而列表中的元素则构成了这一行的各个列。在Python中，二维列表一般用于存储表格数据、矩阵等。

例如，以下是一个简略的二维列表：

```python

matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

在这个比如中，`matrix`是一个3行3列的二维列表，包含了9个整数。

二、创立二维列表

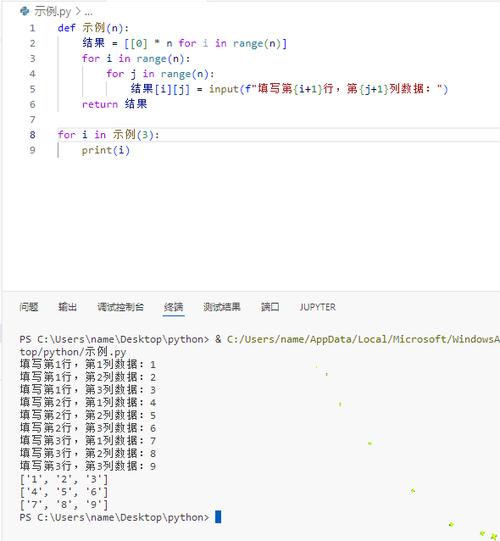
怎么创立二维列表？

在Python中，创立二维列表首要有以下几种办法：

1. 直接初始化：经过直接指定行和列的元从来创立二维列表。

2. 列表推导式：运用列表推导式能够方便地创立具有特定规则的二维列表。

3. 嵌套列表：经过嵌套列表的办法，将多个一维列表组合成二维列表。

```python

办法一：直接初始化

matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

办法二：列表推导式

matrix2 = [[i for i in range(1, 4)] for j in range(3)]

办法三：嵌套列表

matrix3 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

三、操作二维列表

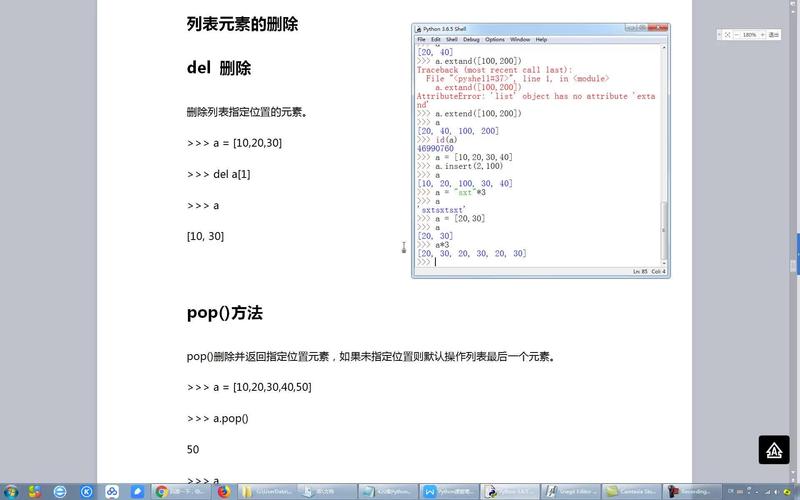
怎么操作二维列表？

二维列表的操作首要包含以下几种：

1. 拜访元素：经过索引拜访二维列表中的元素。

2. 修正元素：修正二维列表中指定方位的元素。

3. 增加和删去行/列：向二维列表中增加或删去行和列。

4. 遍历二维列表：遍历二维列表中的一切元素。

```python

拜访元素

print(matrix1[1][2]) 输出：6

修正元素

matrix1[1][2] = 10

print(matrix1[1][2]) 输出：10

增加行

matrix1.append([11, 12, 13])

print(matrix1) 输出：[[1, 2, 3], [4, 5, 10], [7, 8, 9], [11, 12, 13]]

删去行

del matrix1[2]

print(matrix1) 输出：[[1, 2, 3], [4, 5, 10], [11, 12, 13]]

遍历二维列表

for row in matrix1:

for element in row:

print(element, end=' ')

print()

输出：1 2 3 4 5 10 11 12 13

四、二维列表的运用场景

二维列表在Python中的运用场景

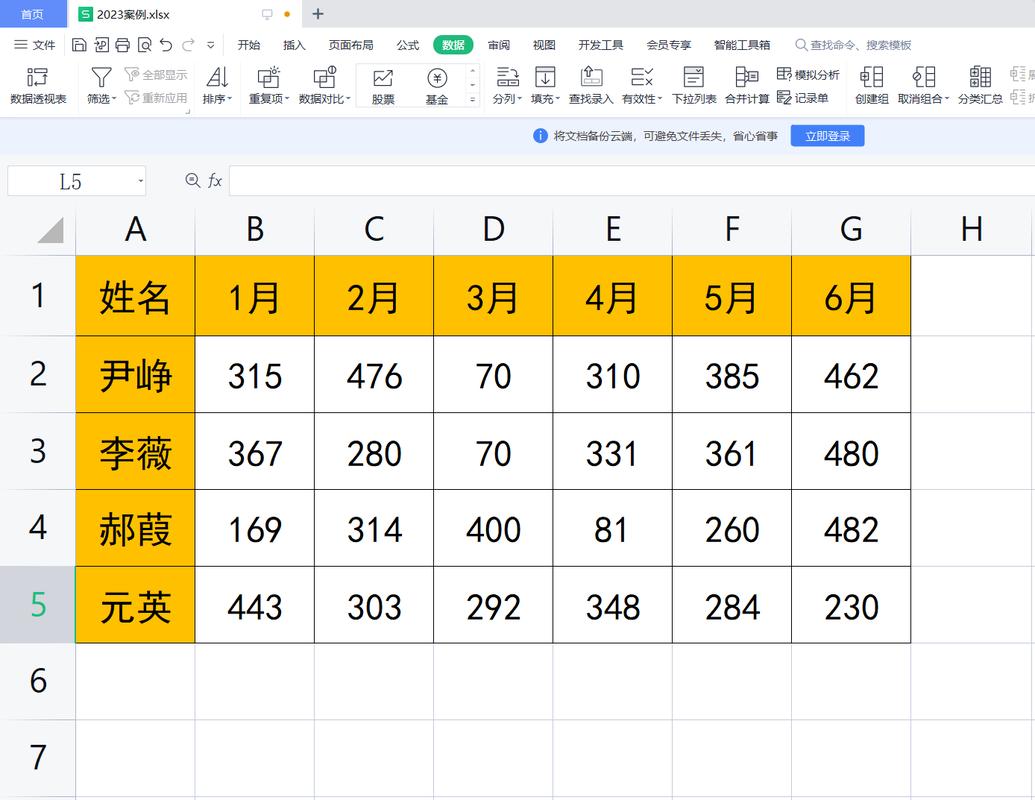
1. 数据处理：用于存储和处理表格数据，如Excel文件中的数据。

2. 图形界面设计：在图形界面设计中，二维列表能够用于存储界面元素的布局信息。

3. 游戏开发：在游戏开发中，二维列表能够用于存储游戏地图、人物方位等信息。

```python

数据处理

data = [[1, 'Alice'], [2, 'Bob'], [3, 'Charlie']]

for row in data:

print(f\