lr机器学习,逻辑回归的原理与运用

LR（Logistic Regression，逻辑回归）是一种用于二分类的监督学习算法。它经过构建一个逻辑函数（Sigmoid函数）来猜测一个样本归于某一类其他概率。在LR中，咱们运用一个线性函数（一般是线性回归的模型）来估量特征与类别之间的权重，然后经过Sigmoid函数将这个线性函数的输出映射到0到1之间，然后得到一个概率值。

LR的优势在于它的模型简略，易于完成和了解，并且具有很好的可解释性。此外，LR还能够经过正则化技能来避免过拟合，进步模型的泛化才能。

LR的局限性在于它假定特征之间是线性联系，这在实践运用中或许并不总是建立。此外，当特征之间存在着杂乱的非线性联系时，LR的功能或许会受到限制。

浅显易懂LR机器学习算法：逻辑回归的原理与运用

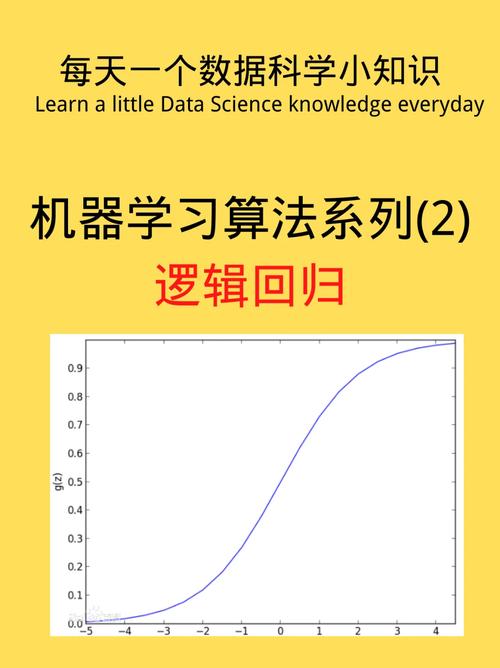
一、逻辑回归的原理

逻辑回归是一种用于处理二分类问题的核算学习办法。其基本思想是，经过一个线性函数的组合，将特征和类别之间的联系建模为一个概率。经过一个逻辑函数（一般是sigmoid函数）将这个概率转化为一个落在0到1之间的数，表明某样本归于某一类其他概率。

二、逻辑回归的公式与丢失函数

逻辑回归的公式如下：

\\[ P(Y=1|X) = \\frac{1}{1 e^{-(\\beta_0 \\beta_1X_1 \\beta_2X_2 ... \\beta_nX_n)}} \\]

其间，\\( P(Y=1|X) \\) 表明在给定特征 \\( X \\) 的条件下，样本归于正类（类别1）的概率；\\( \\beta_0 \\) 和 \\( \\beta_1, \\beta_2, ..., \\beta_n \\) 是模型的参数，需求经过练习数据进行优化。

逻辑回归的丢失函数一般运用穿插熵丢失函数（Cross-Entropy Loss），也称为对数丢失（Log Loss），其公式如下：

\\[ L(\\theta) = -\\frac{1}{m} \\sum_{i=1}^{m} [y_i \\log(\\hat{y}_i) (1 - y_i) \\log(1 - \\hat{y}_i)] \\]

三、逻辑回归的完成办法

逻辑回归的完成办法首要包含以下过程：

数据预处理：对原始数据进行清洗、归一化等操作，进步模型的练习作用。

特征挑选：依据特征的重要性，挑选对模型影响较大的特征，削减核算量。

模型练习：运用梯度下降法（Gradient Descent）或其变种（如随机梯度下降SGD、小批量梯度下降Mini-batch GD）来优化丢失函数，找到最佳的模型参数。

模型评价：运用测验集对模型进行评价，判别模型的功能。

四、逻辑回归的运用事例

逻辑回归在实践运用中具有广泛的运用场景，以下罗列几个事例：

金融范畴：信誉评分、诈骗检测、股票猜测等。

医疗范畴：疾病诊断、药物研制、患者预后等。

电商范畴：用户行为剖析、产品引荐、广告投进等。

交际网络：情感剖析、用户画像、社区引荐等。

逻辑回归作为一种经典的机器学习算法，在分类问题中具有广泛的运用。本文介绍了逻辑回归的原理、公式、完成办法以及运用事例，期望对读者有所协助。在实践运用中，能够依据具体问题挑选适宜的逻辑回归模型，并结合其他机器学习算法进行优化，以进步模型的功能。