筑巢季最新爆料:揭秘鸟类家园的秘密春天来了,万物复苏,又到了一年一度的筑巢季。在这个充满生机与活力的季节里,鸟类们纷纷忙碌起来,为自己的后代搭建温馨的家。今天,就让我们一起揭开鸟类筑巢的神秘面纱,探寻它们家园的秘密。一、筑巢...
-
 吃瓜热榜
吃瓜热榜
筑巢季最新爆料
-
 最新爆料
最新爆料
狂魔哥最新爆料新闻视频,最新爆料新闻视频深度解析
最近网上可是炸开了锅,狂魔哥的最新爆料视频简直成了大家茶余饭后的谈资。这不,我赶紧凑了个热闹,把那些精彩细节都给你一一道来,让你也能跟上这波热点!一、狂魔哥是谁?在说最新爆料之前,咱们得先聊聊这位狂魔哥。你可能不熟悉这个名字...
-
 娱乐新闻
娱乐新闻
蛋仔岛最新爆料视频下载
最近有没有听说蛋仔岛的新鲜事儿?没错,就是那个让人又爱又恨的蛋仔岛,最近又出了个大招!这不,我刚刚从网上找到了一个超级详细的爆料视频,迫不及待地想和你分享一下。快来跟我一起看看吧,保证让你大呼过瘾!一、视频亮点抢先看首先,这...
-
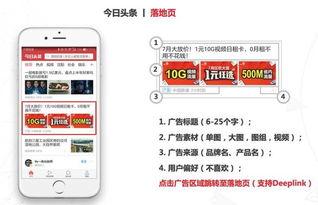 热门大瓜
热门大瓜
今日头条江西爆料电话
你知道吗?最近在江西发生了一件超级劲爆的事情,让人忍不住想要一探究竟。这不,我刚刚从今日头条上了解到,江西的爆料热线可是火得一塌糊涂呢!今天,就让我带你一起来揭秘这个神秘的江西爆料电话,看看它背后隐藏着哪些精彩故事。揭秘江西...
-
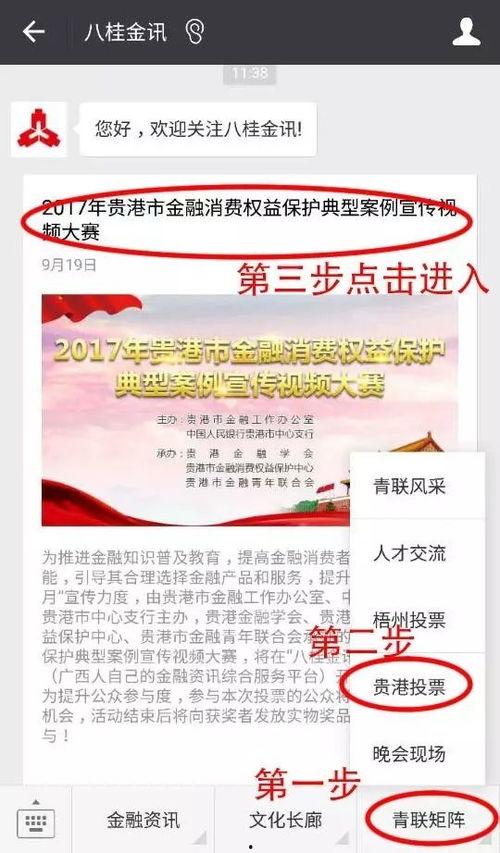 热门大瓜
热门大瓜
贵港最新爆料消息视频大全,视频大全揭秘惊人内幕
最近贵港可是热闹非凡呢!各种新鲜事儿层出不穷,让人忍不住想要一探究竟。这不,小编就为你搜集到了最新爆料消息视频大全,快来看看吧!一、网红打卡地贵港的网红打卡地可是越来越多了,这不,最近就有一个新晋网红地吸引了无数人的目光。它...
-
 网红明星
网红明星
赵丽颖娱乐吃瓜事件视频,揭秘吃瓜视频背后的真相
最近娱乐圈可是热闹非凡呢!赵丽颖这个名字,相信大家都不陌生吧。这不,她最近的一次“吃瓜”事件,可是让网友们炸开了锅。今天,就让我带你一起来八卦看看这位当红小花旦这次都遭遇了些什么吧!一、事件起因:赵丽颖被拍吃瓜视频话说那天,...
-
 最新爆料
最新爆料
火影最新资料爆料视频
火影迷们,是不是已经迫不及待想要了解最新的火影资讯了呢?今天,我就要给你带来一份超级详细的火影最新资料爆料视频,让你一次性看个够!准备好了吗?让我们一起揭开神秘的面纱,探索火影世界的最新动态吧!一、视频亮点抢先看1. 新角色...
-
 热门大瓜
热门大瓜
陆树铭妻子爆料了吗视频,揭秘背后真相
最近娱乐圈可是热闹非凡呢!咱们就来聊聊那位曾经红极一时的演员陆树铭,还有他那神秘的妻子。最近,网络上突然爆出了一段视频,说是陆树铭的妻子爆料了什么大秘密。这可真是让人好奇心爆棚啊!让我们一起揭开这神秘的面纱,看看背后到底隐藏...
-
 吃瓜热榜
吃瓜热榜
新闻爆料视频能卖钱真假,真伪难辨,能否变现之谜
揭秘新闻爆料视频:能卖钱?真假难辨!在这个信息爆炸的时代,新闻爆料视频成为了许多人获取信息的重要途径。它们或揭露真相,或引发热议,甚至有人从中看到了商机。那么,新闻爆料视频真的能卖钱吗?它们的内容又是否真实可信呢?让我们一起...
-
 娱乐新闻
娱乐新闻
女儿们的恋爱在线观看,甜蜜互动,见证青春成长
亲爱的读者们,你是不是也和我一样,对女儿们的恋爱故事充满了好奇呢?最近,一部关于年轻女孩们恋爱生活的电视剧在网上引起了热议,名字叫做《女儿们的恋爱》。这不,我迫不及待地找来这部剧,准备和你一起深入探讨看看这些青春洋溢的女孩们...
