php加密,安全看护您的数据

1. MD5：这是一种常用的哈希算法，用于生成数据的指纹。但MD5已不再被视为安全的加密办法，由于它简单被破解。

2. SHA1：这是另一种哈希算法，比MD5更安全。但相同，它也已被以为不再安全，由于存在已知的磕碰进犯。

3. SHA256：这是SHA2系列算法中的一种，比SHA1更安全。它是现在最常用的哈希算法之一。

4. bcrypt：这是一种专为暗码哈希规划的算法，它包含一个盐值，这使得即便两个相同的暗码也不会发生相同的哈希值。PHP中能够运用`password_hash`和`password_verify`函数来运用bcrypt。

5. Argon2i：这是最新的暗码哈希算法，被规划为反抗GPU加快进犯。PHP中能够运用`password_hash`和`password_verify`函数来运用Argon2i。

6. AES：这是最常用的对称加密算法之一，用于加密宽和密数据。PHP中能够运用`openssl_encrypt`和`openssl_decrypt`函数来运用AES。

7. RSA：这是一种非对称加密算法，用于加密宽和密数据。PHP中能够运用`openssl_public_encrypt`和`openssl_private_decrypt`函数来运用RSA。

8. JWT：这是一种用于在各方之间安全地传输信息的格局。PHP中能够运用`JWT`库来创建和验证JWT。

9. Base64：这是一种编码办法，用于将二进制数据编码为ASCII字符。尽管它不是加密办法，但有时用于传输二进制数据。

10. CURL：这是一种用于在PHP中发送HTTP恳求的办法，能够用于与加密相关的API交互。

11. CURL Multi：这是CURL的扩展，用于一起发送多个HTTP恳求，能够进步与加密相关的API交互的功率。

12. SSL/TLS：这是一种用于在网络上安全地传输数据的协议。PHP中能够运用`openssl`扩展来运用SSL/TLS。

13. PHPMailer：这是一个用于发送电子邮件的PHP库，支撑SSL/TLS加密。

14. Guzzle：这是一个用于发送HTTP恳求的PHP库，支撑SSL/TLS加密。

15. Stripe：这是一个用于处理付出的买卖处理API，支撑SSL/TLS加密。

16. OpenSSL：这是一个用于加密的PHP扩展，供给了多种加密功用。

17. PHPseclib：这是一个用于加密的PHP库，供给了多种加密功用。

18. JWT：这是一个用于在各方之间安全地传输信息的格局。PHP中能够运用`JWT`库来创建和验证JWT。

19. Sodium：这是一个用于加密的PHP扩展，供给了多种加密功用。

20. NaCl：这是一个用于加密的PHP库，供给了多种加密功用。

请留意，挑选加密办法时，应考虑安全性和功能。关于灵敏数据，应运用最新的、最安全的加密算法。一起，应保证加密密钥的安全，避免走漏。

浅显易懂PHP加密技能：安全看护您的数据

一、PHP加密概述

PHP加密技能首要包含对称加密、非对称加密和哈希加密三种类型。对称加密是指加密宽和密运用相同的密钥，如AES、DES等；非对称加密是指加密宽和密运用不同的密钥，如RSA、ECC等；哈希加密则是将数据转换成固定长度的字符串，如MD5、SHA1等。

二、PHP内置加密函数

openssl_encrypt：运用指定的算法和密钥对数据进行加密。

openssl_decrypt：运用指定的算法和密钥对数据进行解密。

hash：生成数据的哈希值。

password_hash：生成暗码的哈希值。

password_verify：验证暗码的哈希值。

三、对称加密实例

以下是一个运用AES-256加密算法的示例：

解密进程如下：

四、非对称加密实例

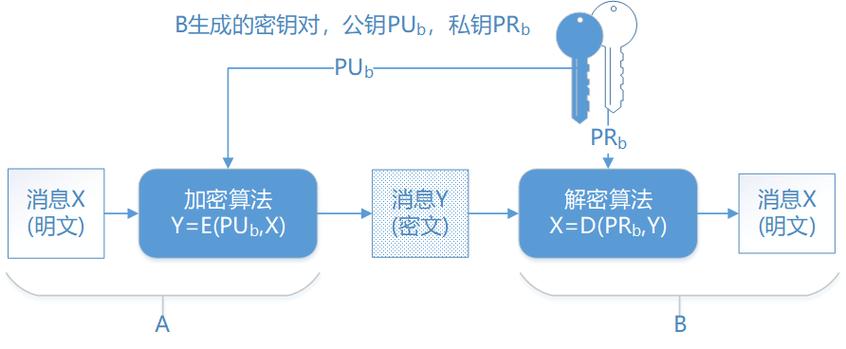
以下是一个运用RSA加密算法的示例：

解密进程如下：

五、哈希加密实例

以下是一个运用SHA256哈希算法的示例：

PHP加密技能为开发者供给了强壮的数据维护东西，能够协助咱们更好地看护数据安全。在实践开发进程中，应根据详细需求挑选适宜的加密算法和函数，保证数据的安全性。一起，也要留意密钥和灵敏信息的安全办理，避免密钥走漏导致数据安全危险。