机器学习 线性回归,深化解析机器学习中的线性回归算法

线性回归是机器学习中最根底和常用的算法之一，它首要用来猜测一个接连的方针变量。线性回归的中心思维是树立一个线性模型来描绘自变量（特征）与因变量（方针变量）之间的联系。

线性回归的基本概念

线性回归模型能够表明为：

$$y = beta_0 beta_1x_1 beta_2x_2 ... beta_nx_n epsilon$$

谈判： $ y $ 是方针变量（因变量）。 $ x_1, x_2, ..., x_n $ 是自变量（特征）。 $ beta_0, beta_1, ..., beta_n $ 是模型的参数，谈判 $ beta_0 $ 是截距，$ beta_1, beta_2, ..., beta_n $ 是各自变量的系数。 $ epsilon $ 是差错项，表明模型无法解释的随机差错。

线性回归的分类

依据自变量的数量，线性回归能够分为以下几类：1. 简略线性回归：只要一个自变量。2. 多元线性回归：有多个自变量。

线性回归的求解办法

线性回归的求解办法首要有以下几种：1. 最小二乘法：经过最小化差错平方和来求解模型参数。2. 梯度下降法：经过迭代优化来求解模型参数。3. 正则化线性回归：在最小二乘法的根底上参加正则化项，避免过拟合。

线性回归的运用

线性回归在许多范畴都有广泛的运用，例如：1. 经济学：猜测房价、股票价格等。2. 金融学：信誉评分、危险评价等。3. 生物医学：疾病猜测、药物作用剖析等。4. 工程学：设备毛病猜测、资料功能剖析等。

线性回归的局限性

线性回归也有其局限性，首要绵亘：1. 假定自变量与因变量之间存在线性联系。2. 对异常值灵敏。3. 无法处理非线性联系。

尽管如此，线性回归仍然是一种简略、有用且广泛运用的机器学习算法。在实践运用中，能够依据具体问题挑选适宜的线性回归模型和求解办法。

深化解析机器学习中的线性回归算法

线性回归是机器学习和统计学中最根底且运用广泛的猜测建模技能之一。本文将具体介绍线性回归的根底知识、算法原理、中心概念、完成办法以及其在实践问题中的运用。

一、线性回归的界说与根底

线性回归是一种用于建模方针变量（因变量）和一个或多个猜测变量（自变量）之间线性联系的技能。方针是经过一个线性方程来表达这种联系，从而对新的数据进行猜测。

二、线性回归的线性方程

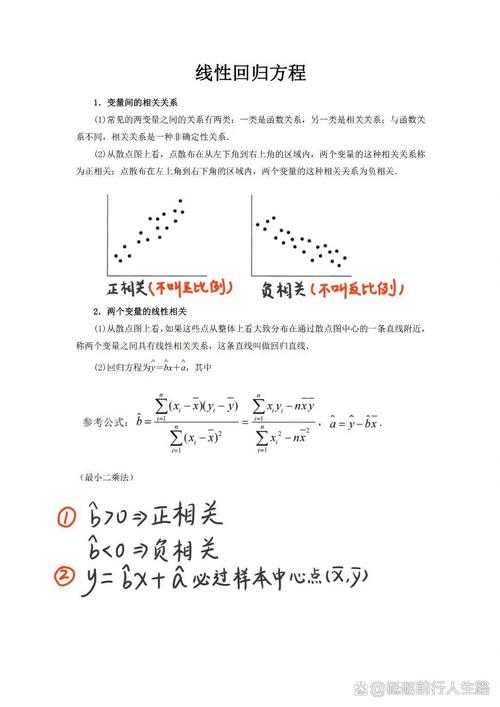
线性回归模型能够表明为以下两种方式：

1. 简略线性回归（只要一个自变量）：

y = beta0 beta1 x epsilon

谈判：y 是因变量，x 是自变量，beta0 是截距，beta1 是斜率系数，epsilon 是差错项。

2. 多元线性回归（有多个自变量）：

y = beta0 beta1 x1 beta2 x2 ... betan xn epsilon

谈判：y 是因变量，x1, x2, ..., xn 是自变量，beta0 是截距，beta1, beta2, ..., betan 是斜率系数，epsilon 是差错项。

三、线性回归的假定

线性回归模型根据以下假定：

1. 线性联系：自变量和因变量之间的联系有必要是线性的。

2. 独立性：每个调查值之间彼此独立。

3. 同方差性（Homoscedasticity）：差错项的方差应保持一致。

4. 正态性：差错项应遵守正态分布。

5. 无多重共线性：关于多元线性回归，自变量之间不应该高度相关。

四、线性回归的算法原理与中心

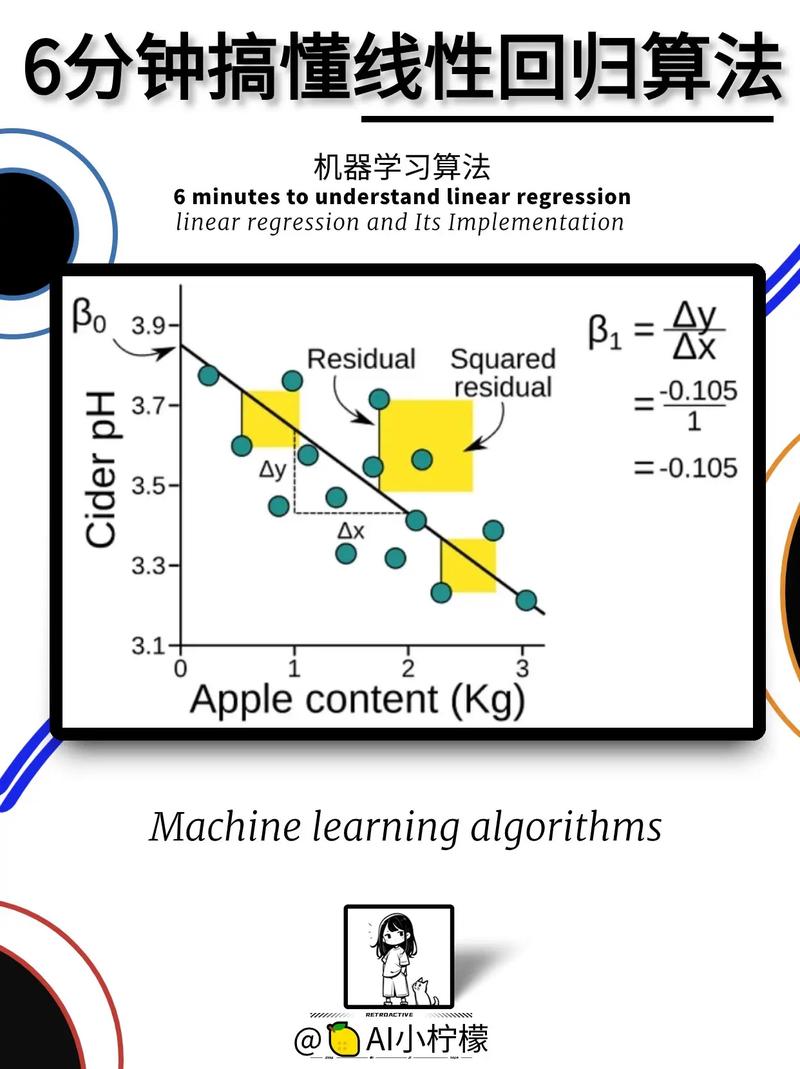
线性回归经过最小化残差平方和（Sum of Squared Residuals, SSR）来估量模型参数。残差是指实践观测值与模型猜测值之间的差异。残差平方和越小，阐明模型拟合度越好。

残差平方和的核算公式如下：

SSR = Σ(yi - y?i)^2

谈判：yi 是实践观测值，y?i 是模型猜测值。

五、线性回归的完成办法

线性回归能够经过多种办法完成，以下罗列几种常见办法：

1. 最小二乘法（Ordinary Least Squares, OLS）：经过最小化残差平方和来估量模型参数。

2. 梯度下降法（Gradient Descent）：经过迭代优化模型参数，使残差平方和最小化。

3. 随机梯度下降法（Stochastic Gradient Descent, SGD）：在梯度下降法的根底上，每次迭代只运用一个样本，进步核算功率。

六、线性回归在实践问题中的运用

线性回归在许多实践问题中都有广泛的运用，以下罗列几个比如：

1. 房价猜测：经过剖析房子的特征（如面积、地段等），猜测房子的价格。

2. 活动油耗猜测：经过剖析活动的参数（如排量、分量等），猜测活动的油耗。

3. 信誉评分：经过剖析个人的信誉前史，猜测其信誉危险。

线性回归是机器学习和统计学中最根底且运用广泛的猜测建模技能。经过本文的介绍，信任读者对线性回归有了更深化的了解。在实践运用中，合理挑选线性回归模型，并对其进行优化，能够协助咱们更好地处理实践问题。