机器学习 数学,探究数据与算法的桥梁

机器学习和数学是密切相关的范畴。在机器学习中，数学是构建和练习模型的根底，是了解和剖析模型功能的要害东西。以下是机器学习与数学之间的一些首要联络：

1. 线性代数：线性代数是机器学习的根底，由于它供给了处理多维数据的办法。向量、矩阵和线性改换是线性代数的要害概念，它们在机器学习中用于表明数据、构建模型和进行核算。

2. 概率论和计算学：概率论和计算学是了解数据不确定性和随机性的要害。在机器学习中，这些概念用于构建模型、估量参数、评价模型功能和进行猜测。

3. 微积分：微积分在机器学习中用于优化模型参数。梯度下降是一种常用的优化算法，它依据微积分中的导数概念。

4. 概率图模型：概率图模型是一种强壮的东西，用于表明和推理杂乱概率联系。它们在机器学习中用于构建杂乱模型，如贝叶斯网络和马尔可夫链。

5. 最优化理论：最优化理论是机器学习中的一个重要分支，它重视于找到函数的最大值或最小值。最优化算法，如梯度下降和随机梯度下降，用于练习机器学习模型。

6. 信息论：信息论是研讨信息传递和编码的理论。在机器学习中，信息论用于评价模型的杂乱性和信息增益。

7. 数值剖析：数值剖析是研讨数值办法和算法的理论。在机器学习中，数值剖析用于完成和优化算法，如求解线性方程组和优化问题。

8. 逻辑和集合论：逻辑和集合论是数学的根底，它们在机器学习中用于表明和推理常识。例如，逻辑回归是一种依据逻辑的机器学习算法。

9. 几何学：几何学在机器学习中用于处理空间数据，如图画和视频。几何学概念，如间隔、形状和改换，在机器学习中用于特征提取和模型构建。

10. 拓扑学：拓扑学是研讨空间结构和性质的理论。在机器学习中，拓扑学用于剖析数据结构和辨认模式。

总归，数学是机器学习的根底，它供给了构建、练习和剖析模型所需的东西和办法。关于想要深化了解机器学习的人来说，把握数学常识是非常重要的。

机器学习中的数学根底：探究数据与算法的桥梁

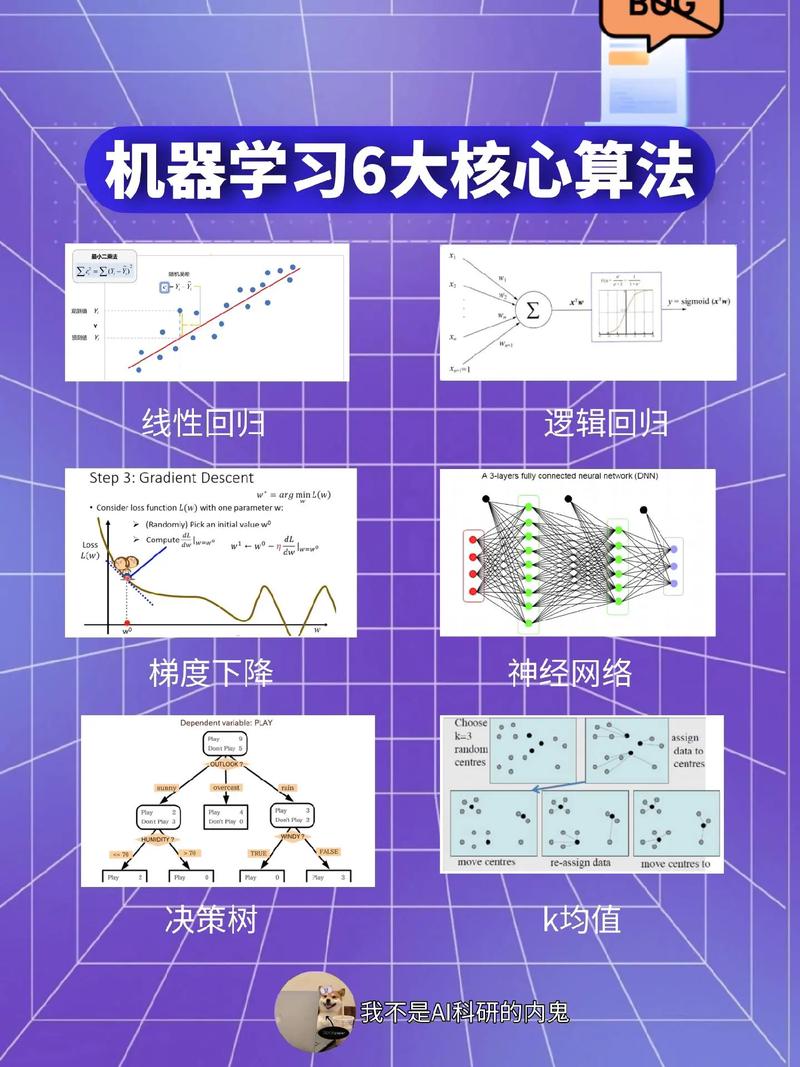
概率论与数理计算：机器学习的柱石

概率论和数理计算是机器学习中的两大柱石。概率论为机器学习供给了描绘不确定性的言语，而数理计算则供给了从数据中提取信息的办法。

在机器学习中，概率论用于描绘数据散布、模型参数的先验散布以及猜测成果的置信度。例如，贝叶斯定理是概率论在机器学习中的一个重要使用，它能够协助咱们依据先验常识和观测数据更新模型参数的信仰。

数理计算则供给了从样本数据中估量整体参数的办法。例如，假设检验、置信区间和假设检验等计算办法能够协助咱们判别模型是否具有计算显著性。

线性代数：矩阵与向量的国际

线性代数是机器学习中不可或缺的东西，它涉及到矩阵、向量、线性改换等概念。在机器学习中，线性代数被广泛使用于特征提取、降维、优化等方面。

矩阵和向量是线性代数中的基本概念，它们在机器学习中扮演着重要人物。例如，在主成分剖析（PCA）中，经过求解协方差矩阵的特征值和特征向量，能够完成对数据的降维。

线性改换是线性代数中的另一个重要概念，它能够将数据从一种表明办法转换为另一种表明办法。例如，在神经网络中，权重矩阵和偏置向量构成了线性改换，它们决议了输入数据在神经网络中的传达办法。

优化理论：寻觅最优解的旅程

优化理论是机器学习中处理优化问题的中心东西。在机器学习中，优化问题一般涉及到寻觅模型参数的最优值，以完成猜测或分类的准确性。

优化理论供给了多种算法来处理优化问题，如梯度下降、牛顿法、共轭梯度法等。这些算法经过迭代更新模型参数，逐渐迫临最优解。

在机器学习中，优化问题一般与丢失函数相关联。丢失函数用于衡量模型猜测成果与实在值之间的差异，优化算法的方针是找到使丢失函数最小的模型参数。

信息论：数据与常识的衡量

信息论是研讨信息传输、存储和处理的理论。在机器学习中，信息论供给了衡量数据杂乱性和信息量的办法，有助于咱们了解数据背面的规则。

信息熵是信息论中的一个重要概念，它用于衡量数据的随机性和不确定性。在机器学习中，信息熵能够协助咱们挑选适宜的特征，以下降模型的杂乱性和进步猜测准确性。

互信息是另一个重要的信息论概念，它用于衡量两个变量之间的相关性。在机器学习中，互信息能够协助咱们辨认数据中的潜在联系，然后进步模型的功能。

数学作为机器学习的根底，为算法供给了坚实的理论根底和强壮的东西。从概率论和数理计算到线性代数、优化理论和信息论，数学在机器学习中扮演着不可或缺的人物。跟着机器学习技能的不断发展，数学在机器学习中的使用将愈加广泛和深化。