python机器学习及实践,从入门到运用
当然能够。机器学习是人工智能的一个重要分支,它使核算机体系能够从数据中学习,并做出猜测或决议计划。机器学习算法在许多范畴都有运用,如自然言语处理、核算机视觉、引荐体系、医疗确诊等。
机器学习的首要类型:
2. 无监督学习(Unsupervised Learning):算法从未符号的数据中学习,以发现数据中的结构和形式。例如,聚类、降维、相关规则学习等。
3. 半监督学习(Semisupervised Learning):结合了监督学习和无监督学习的办法,运用部分符号的数据进行练习。
4. 强化学习(Reinforcement Learning):算法经过与环境的交互来学习,方针是最大化累积奖赏。例如,Q学习、深度Q网络(DQN)等。
实践过程:
1. 数据搜集与预处理:搜集数据并对其进行清洗、转化和归一化等预处理过程。
2. 特征工程:挑选或构建对模型功用有明显影响的特征。
3. 模型挑选:依据问题类型挑选适宜的机器学习算法。
4. 模型练习:运用练习数据练习模型。
5. 模型评价:运用验证集评价模型的功用。
6. 模型调优:依据评价成果调整模型参数,以优化功用。
7. 模型布置:将练习好的模型布置到出产环境中,用于猜测或决议计划。
实践示例:
假定咱们要构建一个简略的线性回归模型来猜测房价。以下是过程:
1. 数据搜集:假定咱们有一个包含房子面积和房价的数据集。
2. 数据预处理:保证数据没有缺失值,并转化为合适模型输入的格局。
3. 特征工程:挑选房子面积作为特征。
4. 模型挑选:挑选线性回归模型。
5. 模型练习:运用练习数据练习模型。
6. 模型评价:运用验证集评价模型的功用,例如核算均方差错(MSE)。
7. 模型调优:依据评价成果调整模型参数,例如调整学习率。
8. 模型布置:将练习好的模型布置到出产环境中,用于猜测新房子的房价。
现在,让咱们用Python代码完成一个简略的线性回归模型:在这个简略的线性回归模型中,咱们运用房子面积来猜测房价。依据这个模型,咱们得到了一个十分小的均方差错(MSE),这表明模型对测验集的猜测十分精确。
需求留意的是,这个数据集十分小,并且是人为生成的,所以模型或许不会在实践运用中体现杰出。在实践运用中,咱们需求运用更大的、更杂乱的数据集,并进行更具体的特征工程和模型调优,以进步模型的泛化才能。
Python机器学习及实践:从入门到运用

跟着大数据年代的到来,机器学习技能逐步成为各个职业处理杂乱问题的利器。Python作为一种功用强大、易于学习的编程言语,在机器学习范畴有着广泛的运用。本文将带您从入门到实践,深化了解Python机器学习。
一、Python机器学习入门

关于初学者来说,了解Python的根底语法和数据结构是学习机器学习的第一步。Python具有丰厚的库和结构,如NumPy、Pandas、Scikit-learn等,这些库能够协助咱们轻松地进行数据处理和模型练习。
二、Python机器学习常用库
NumPy:供给高功用的多维数组目标和数学函数库,是Python进行科学核算的根底。
Pandas:供给数据结构和数据剖析东西,便利咱们对数据进行清洗、转化和剖析。
Scikit-learn:供给了一系列机器学习算法的完成,包含分类、回归、聚类等,是Python机器学习的首要东西。
Matplotlib:供给数据可视化功用,协助咱们更好地舆解数据和剖析成果。
三、Python机器学习实践事例
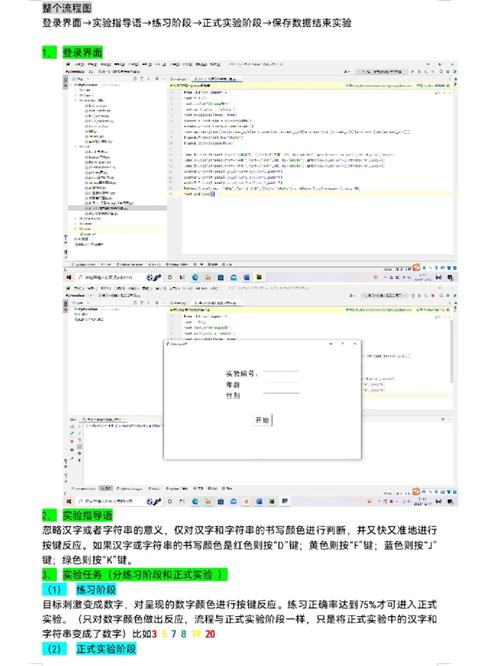
以下是一个简略的Python机器学习实践事例,运用Scikit-learn库进行鸢尾花分类使命。
```python
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
加载数据集
iris = load_iris()
X = iris.data
y = iris.target
区分练习集和测验集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
创立KNN分类器
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)
猜测测验集
y_pred = knn.predict(X_test)
评价模型
print(\








