机器学习线性回归,二、线性回归原理
线性回归是机器学习中最根本的算法之一,用于猜测接连数值型输出。它假定输入特征和输出之间存在线性联系,即输出是输入特征的线性组合。线性回归的方针是找到最佳拟合直线,使得猜测值与实践值之间的差错最小。
线性回归能够分为两种类型:简略线性回归和多元线性回归。
1. 简略线性回归:只要一个自变量和一个因变量,办法为 y = mx b,其间 m 是斜率,b 是截距。
2. 多元线性回归:有多个自变量和一个因变量,办法为 y = b0 b1x1 b2x2 ... bnxn,其间 b0 是截距,b1, b2, ..., bn 是各自变量的系数。
线性回归的求解办法有多种,其间最常见的是最小二乘法。最小二乘法的方针是最小化猜测值与实践值之间的平方差错之和。
线性回归的使用十分广泛,例如:
猜测房价、股票价格等接连数值型输出。 剖析变量之间的联系,例如收入与教育程度之间的联系。 构建特征挑选模型,用于降维和特征提取。
线性回归也有一些局限性,例如:
假定输入特征和输出之间存在线性联系,但实践上或许存在非线性联系。 对异常值灵敏,异常值或许会对模型发生较大影响。 难以处理特征之间的交互作用。
因而,在实践使用中,需求依据具体问题挑选适宜的回归算法。
深化解析机器学习中的线性回归算法
机器学习,线性回归,核算办法,猜测模型,数据剖析
线性回归是机器学习中一种十分根底的核算办法,首要用于猜测接连型变量。在很多机器学习算法中,线性回归因其简略、直观和易于完成的特色,被广泛使用于各个领域。本文将深化解析线性回归算法的原理、完成办法以及在实践使用中的留意事项。
二、线性回归原理
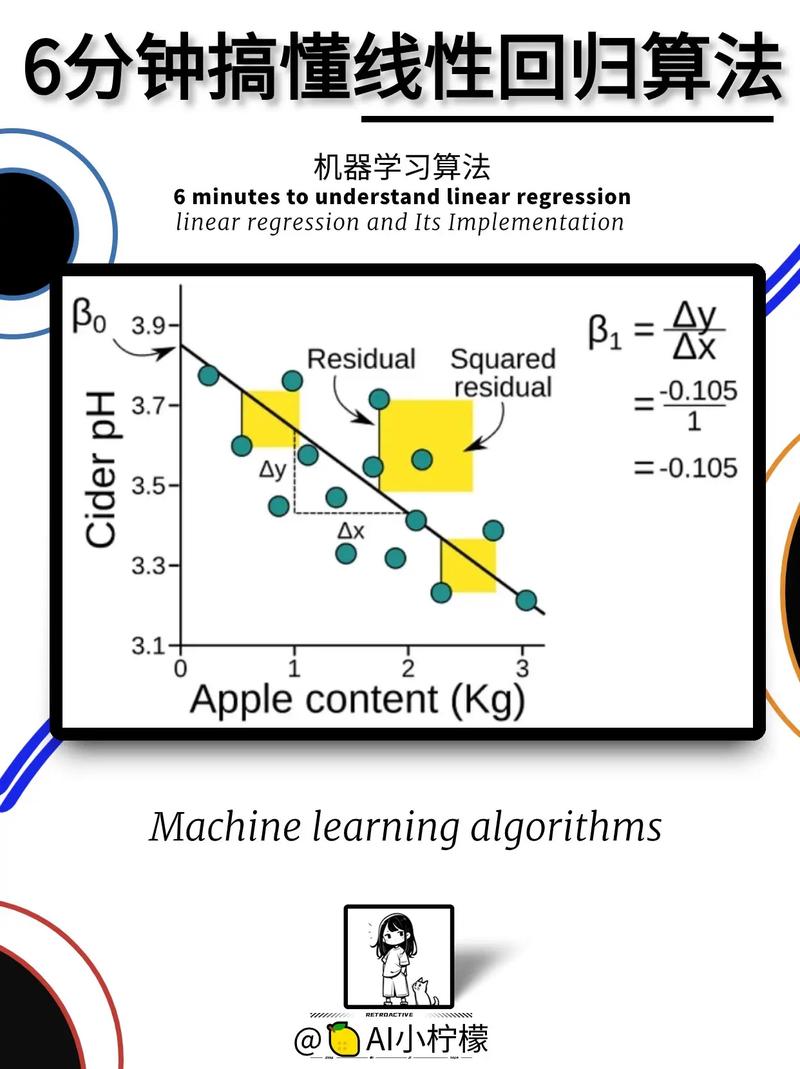
线性回归的方针是找到一个线性模型,该模型能够描绘因变量与自变量之间的联系。具体来说,线性回归假定因变量与自变量之间存在线性联系,即:
Y = β0 β1X1 β2X2 ... βnXn ε
其间,Y为因变量,X1, X2, ..., Xn为自变量,β0为截距,β1, β2, ..., βn为系数,ε为差错项。
线性回归的中心使命是经过学习练习数据,找到最佳的系数β0, β1, ..., βn,使得猜测值与实在值之间的差错最小化。
三、线性回归完成办法

线性回归的完成办法首要有最小二乘法、梯度下降法等。
1. 最小二乘法
最小二乘法是一种常用的线性回归完成办法,其根本思想是找到一组参数,使得因变量与自变量之间的差错平方和最小。具体过程如下:
核算每个数据点的猜测值与实在值之间的差错。
核算差错的平方和。
对系数进行优化,使得差错平方和最小。
2. 梯度下降法
梯度下降法是一种迭代优化算法,经过不断调整参数,使得丢失函数逐步减小。在线性回归中,梯度下降法能够用来求解系数β0, β1, ..., βn。具体过程如下:
初始化系数β0, β1, ..., βn。
核算丢失函数关于每个系数的梯度。
依据梯度调整系数,使得丢失函数减小。
重复过程2和3,直到满意中止条件。
四、线性回归在实践使用中的留意事项
线性回归在实践使用中需求留意以下几点:
1. 数据预处理
在进行线性回归之前,需求对数据进行预处理,包含缺失值处理、异常值处理、特征缩放等。
2. 特征挑选
特征挑选是线性回归中的一个重要环节,挑选适宜的特征能够进步模型的猜测精度。常用的特征挑选办法有单变量特征挑选、逐步回归等。
3. 模型评价
模型评价是线性回归中的关键过程,常用的评价目标有均方差错(MSE)、均方根差错(RMSE)、决定系数(R2)等。
4. 模型调优
模型调优是进步模型猜测精度的重要手法,能够经过调整模型参数、挑选不同的回归办法等办法进行。
线性回归是一种简略、直观且易于完成的机器学习算法,在各个领域都有广泛的使用。本文对线性回归的原理、完成办法以及在实践使用中的留意事项进行了具体解析,期望对读者有所协助。
机器学习,线性回归,核算办法,猜测模型,数据剖析





