杨辉三角c言语,杨辉三角的原理与特色
杨辉三角(也称为帕斯卡三角形)是一个闻名的数学三角阵列,它有广泛的数学运用。下面是一个用C言语完成的杨辉三角的生成办法:
```cinclude
// 函数声明void printPascalTriangle;
int main { int n; printf; scanf; printPascalTriangle; return 0;}
// 函数界说void printPascalTriangle { int arr; for { for { // 榜首行或每行的榜首个数是1 if arr = 1; else // 其他数是上一行的两个数之和 arr = arr arr; printfqwe2; } printf; }}```
这段代码首要界说了一个二维数组 `arr`,用来存储杨辉三角的每一行的值。它经过嵌套循环生成杨辉三角。外层循环操控行数,内层循环操控每行中的数字。每行的榜首个和最终一个数字是1,其他数字是上一行相邻两个数字的和。
用户输入想要生成的杨辉三角的行数,然后程序会打印出相应巨细的杨辉三角。
杨辉三角,又称为帕斯卡三角形,是一种常见的数列摆放,其结构漂亮,规律性强。在数学、核算机科学等范畴有着广泛的运用。本文将具体介绍杨辉三角的原理、特色以及C言语完成办法。
杨辉三角的原理与特色
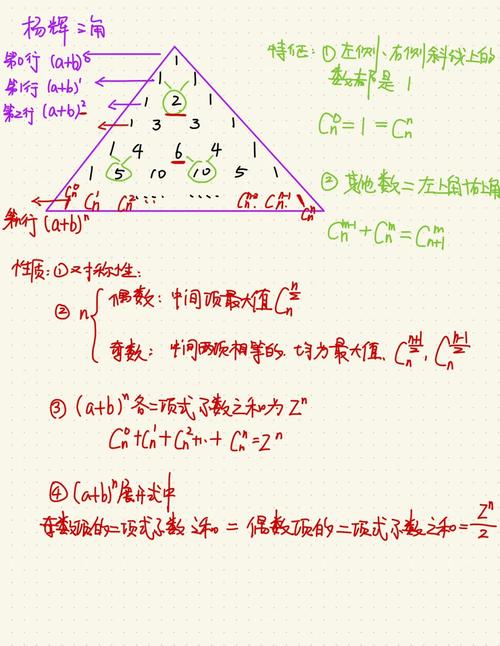
杨辉三角的每一行都由1开端,每个数都是它上方两个数之和。具体来说,第n行的第k个数等于第n-1行的第k-1个数和第k个数之和。杨辉三角具有以下特色:
第0行只要一个数,即1。
第1行有两个数,即[1, 1]。
从第2行开端,每个数都是上一行相邻两个数之和。
鸿沟上的数一直为1。
杨辉三角的数学性质

杨辉三角具有许多风趣的数学性质,以下罗列几个:
杨辉三角的恣意一行都是二项式定理的展开式。
杨辉三角的恣意一行的和等于2的n次方,其间n为行数。
杨辉三角的恣意一行的第k个数等于组合数C(n-1, k-1)。
C言语完成杨辉三角
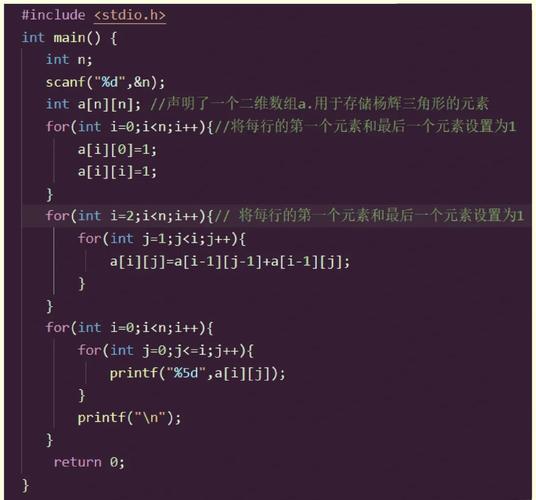
下面是运用C言语完成杨辉三角的代码示例:
```c
include
define MAX_ROWS 10
void printPascalTriangle(int numRows) {
int triangle[MAX_ROWS][MAX_ROWS] = {0};
// 初始化杨辉三角的榜首行和第二行
triangle[0][0] = 1;
triangle[1][0] = 1;
triangle[1][1] = 1;
// 核算杨辉三角的其他行
for (int i = 2; i < numRows; i ) {
triangle[i][0] = 1; // 每行的榜首个数是1
for (int j = 1; j <= i; j ) {
triangle[i][j] = triangle[i - 1][j - 1] triangle[i - 1][j]; // 核算当时数
}
}
// 打印杨辉三角
for (int i = 0; i < numRows; i ) {
for (int j = 0; j <= i; j ) {
printf(\








