电视剧迷们,有没有一部剧让你一刷再刷,回味无穷?今天,我要给你安利一部最近在网络上掀起热潮的电视剧——《老酒馆》。这部剧不仅剧情引人入胜,而且在线观看资源丰富,让你随时随地都能沉浸在老酒馆的故事里。下面就让我带你多角度了解一...
-
 最新爆料
最新爆料
老酒馆电视剧在线观看,岁月流转,酒香依旧,重温民国风情岁月
-
 最新爆料
最新爆料
居哥最新爆料新闻视频播放,最新爆料新闻视频深度解析
你知道吗?最近网上炒得沸沸扬扬的,居哥的最新爆料新闻视频播放量简直爆表了!这可真是让人好奇不已,究竟是什么内容能让这么多人趋之若鹜呢?下面就让我带你一探究竟吧!一、视频内容揭秘居哥,这位在娱乐圈中颇具影响力的明星,这次又带来...
-
 娱乐头条
娱乐头条
哑舍最新爆料4月2日
你知道吗?最近网上可是炸开了锅,大家都在热议《哑舍》的最新爆料!没错,就是那个让我们熬夜追更的《哑舍》,这次竟然在4月2日带来了超级大惊喜!下面,就让我带你一起揭开这个神秘面纱,看看这次爆料都有哪些亮点吧!一、剧情大揭秘:新...
-
 娱乐新闻
娱乐新闻
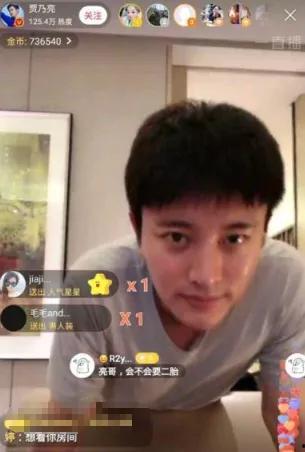
狗仔爆料王子奇视频,王子奇私密视频曝光,真相揭秘
最近娱乐圈可是热闹非凡呢!这不,狗仔队们又爆出了一个大瓜——王子奇的视频!这可真是让人好奇心爆棚,咱们一起来探究一下这个视频背后的故事吧!一、视频内容揭秘首先,让我们来一睹为快,这个视频究竟有什么内容。据狗仔队透露,视频中王...
-
 娱乐头条
娱乐头条
周一大爆料视频
你知道吗?最近网上可是炸开了锅,一大波爆料视频在周一大放异彩,简直让人目不暇接!这些视频从不同角度、不同领域,揭示了各种鲜为人知的秘密,让人看得热血沸腾。下面就让我带你一起揭秘这些周一大爆料的精彩瞬间吧!一、娱乐圈的“秘密花...
-
 最新爆料
最新爆料
敬祺青橙爆料完整视频,独家内幕大公开
最近网上可是炸开了锅,大家都在热议一个视频,那就是传说中的“敬祺青橙爆料完整视频”。这视频里到底有什么秘密?怎么就引起了这么大的关注呢?咱们一起来一探究竟吧!一、视频背景揭秘首先,得说说这个敬祺青橙。原来,这可不是什么神秘人...
-
 娱乐头条
娱乐头条
吃瓜影视免费下载安装,免费下载安装,畅享海量影视资源
你有没有发现,最近网上又掀起了一股“吃瓜”热潮?没错,就是那种一边追剧一边吃瓜,一边吐槽一边笑得前俯后仰的感觉。而说到追剧,不得不提的就是那些让人欲罢不能的影视作品。今天,就让我带你一起探索如何轻松吃瓜,免费下载安装影视AP...
-
 网红明星
网红明星
网友爆料素材视频大全最新,最新素材视频大全,精彩瞬间一网打尽!
最近网上可是热闹非凡呢!各种网友爆料素材视频大全层出不穷,简直让人眼花缭乱。今天,就让我带你一起走进这个奇妙的网络世界,看看都有哪些新鲜事儿吧!一、搞笑瞬间,笑出腹肌首先得说说那些让人捧腹大笑的搞笑视频。网友们可是把生活中的...
-
 娱乐新闻
娱乐新闻
七月航线大爆料最新消息,最新航线信息抢先看
七月航线大爆料:揭秘最新航线动态,带你飞向梦想之地!夏日炎炎,正是出行的好时节!你是否已经迫不及待地想要规划一次说走就走的旅行?别急,且听我细细道来,七月航线大爆料,带你领略最新航线动态,让你轻松飞向梦想之地!一、热门航线盘...
-
 最新爆料
最新爆料
我靠吃瓜征服娱乐圈,揭秘如何用吃瓜技巧征服娱乐圈
你知道吗?在这个信息爆炸的时代,娱乐圈可是个热闹非凡的地方。而我,一个普通的吃瓜群众,竟然凭借吃瓜的本事,在娱乐圈里混得风生水起。是不是觉得有点不可思议?那就让我来给你娓娓道来,看看我是如何靠吃瓜征服娱乐圈的!一、吃瓜起源:...
